Transition Matrix Method
for Polymers Confined to a Lattice, Part 2

The behavior of polymers in solution and at interfaces is of great importance, both from a theoretical point of view and for practical applications. In many cases, the polymers are modeled as quasi-crystalline lattice chains.^1-7

As has been shown in part 1, many statistical properties of confined lattice polymer chains may be calculated from the end segment probabilties, G(N, i), using a transition matrix formalism originally developed by DiMarzio and Roe.^3,4 For example, the conformational partition function Q_N+1 of a lattice polymer is given by

where U^T is the row vector (1, 1, ... 1), G(N) is the column vector of all end segment probabilities, G(N,i), and W is the transition probability matrix. With these functions and the methods of statistical physics many other mean conformational properties can be calculated. For example, the mean position of the last segment is given by

and the density distribution of the last repeat unit

here M is the layer vector (0, 1l, 2l,...,Ml), and E_x is the unitvector (0, ...0, 1, 0,..., 0).
The mean number of steps ν(0,χ_s,N) in the surface layer of an N-step walk can be calculated from³

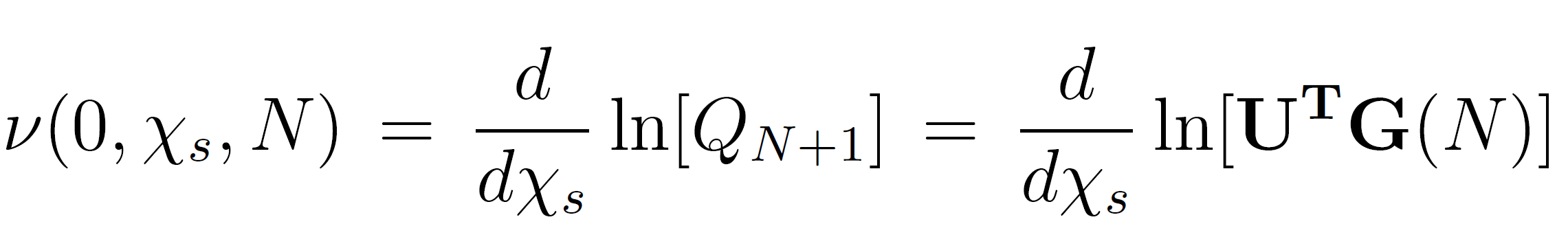
In this equation, the function e^χ_s serves as a counting variable under the operation d/dχ_s. The average number of steps in the other layers can be calculated in a similar way, if we modify the recurrence equations as follows:

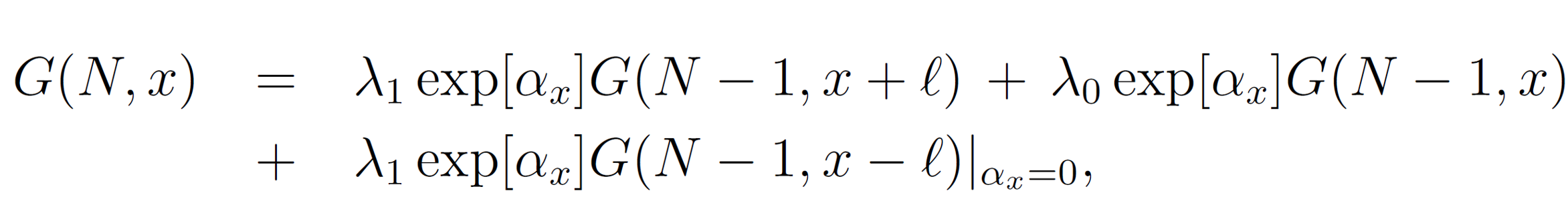
where the counting variable α_x is assumed to be infinitesimal small. The analogous expression for ν(0,χ_s,N) is

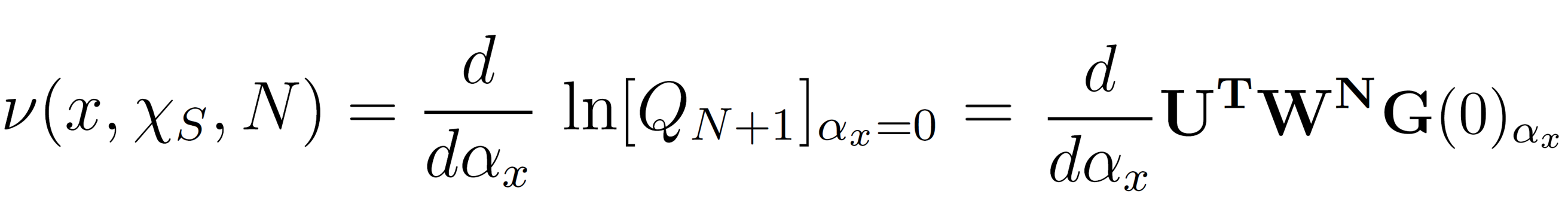
G(0)_αx is a modified starting vector:

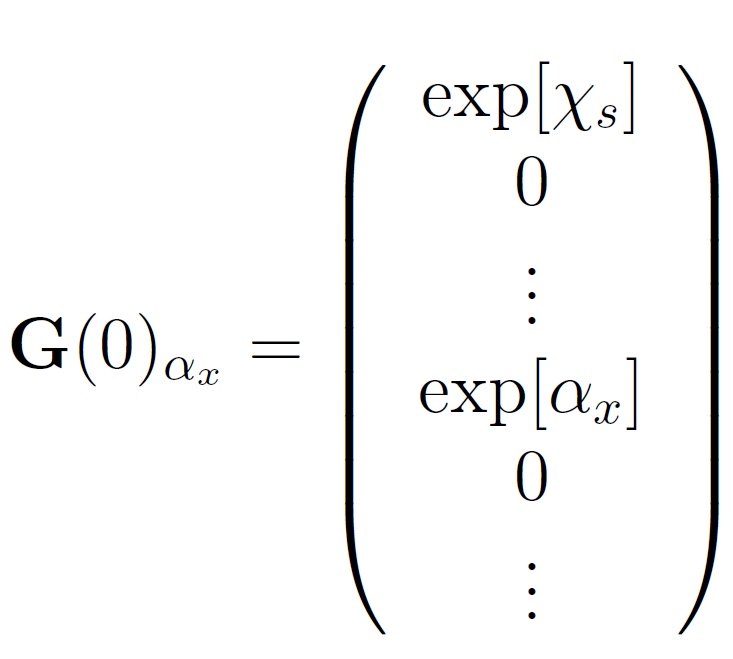
In the case of not too large N, the expressions above can be easily evaluated on a computer. By performing the differentiation we obtain

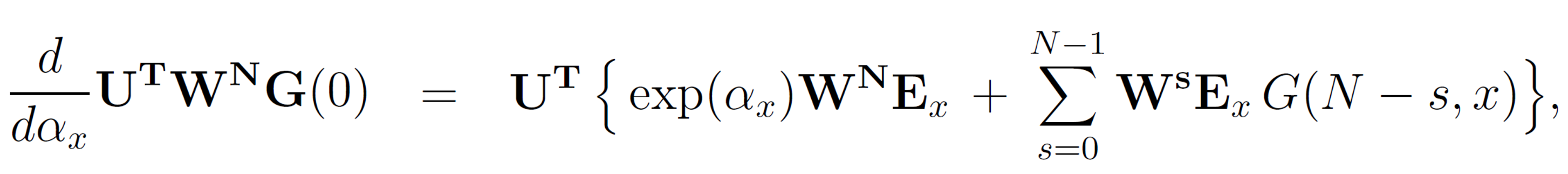
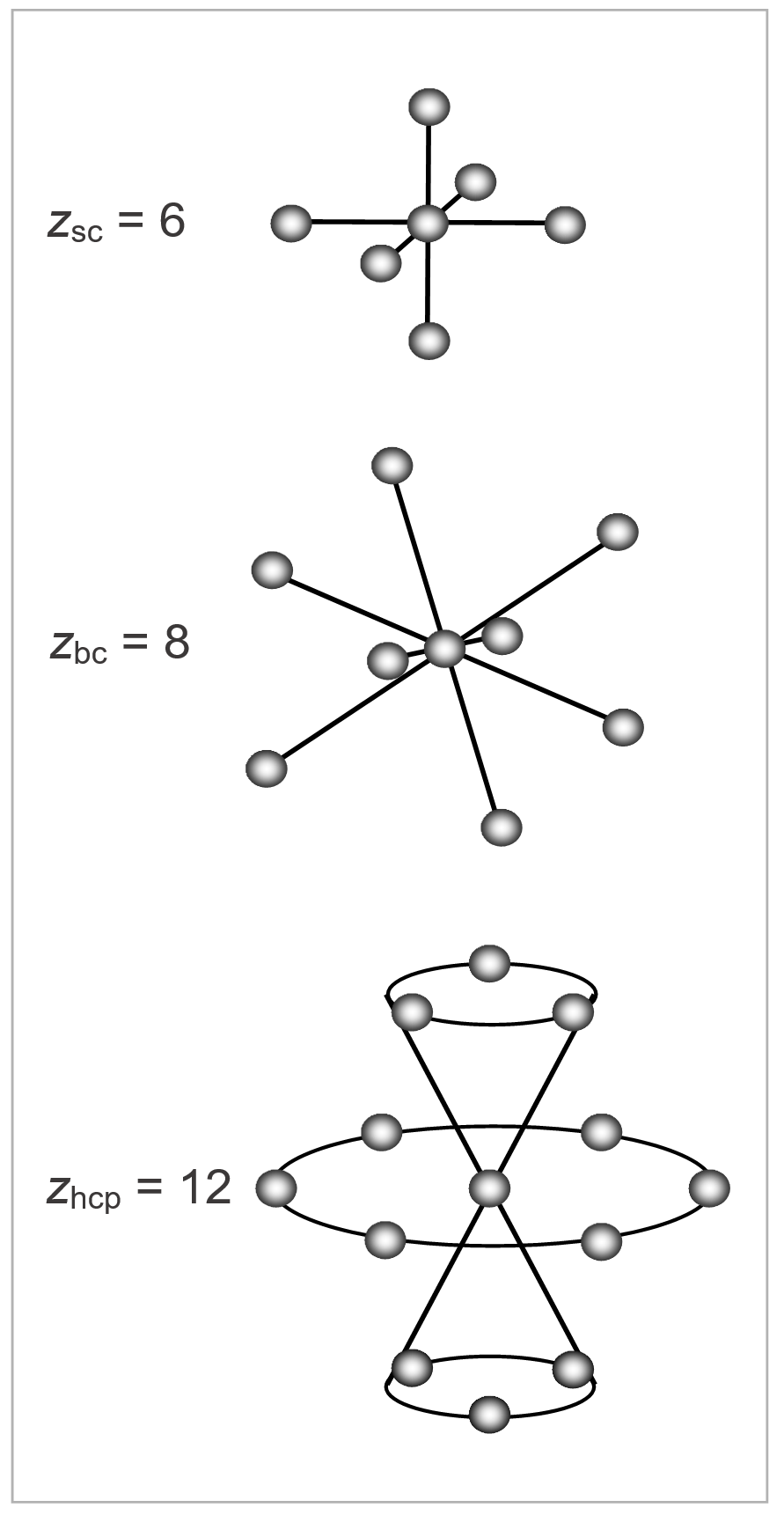
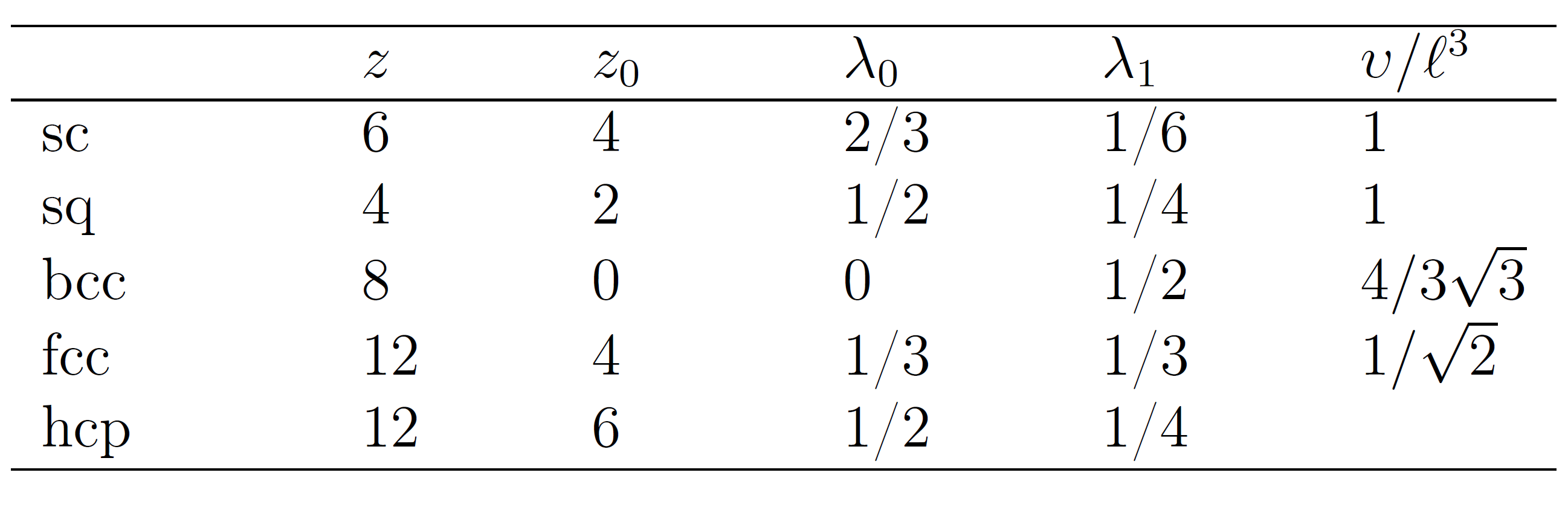
where G(N-s,x) is the (N-s)th component of W^N-sG(0) and E_x the (N-s)th unit vector. The components of G(s,x) are easily evaluated and summed. The results depend on the chosen lattice. The lattice parameters of some of the most common lattices are listed in the Table below.

Lattice Parameters of some Common Lattices

 

As has been shown by DiMarzio, Guttman and Mah⁴, the matrix method can also be applied to other polymer architectures than homopolymer such as stars and (random or block) copolymers. For example, in the case of an AB-copolymer, the only change is that the matrices W_A and W_B in the equations above appear as a product in the same sequence as in the copolymer. For example, suppose there are r - s A-type monomers followed by s B-type and that this sequence is repeated N times in the polymer chain, the conformational partition function reads

where the matrices W_A and W_B are alike except that χ_s,A replaces χ_s,B. The extension to random copolymers is quite obvious. If the polymer has the exact sequence AABAB..., then the partition function of the polymer is

In the case of star polymers with f branches, the partition function Q_N+1 is somewhat more complicated. Let Q(i; m; N_a,i) be the partition function of the ith branch, which consists of N_a,i segments and starts in the mth layer, then the partition function of the whole star-shaped polymer chain is given by⁴

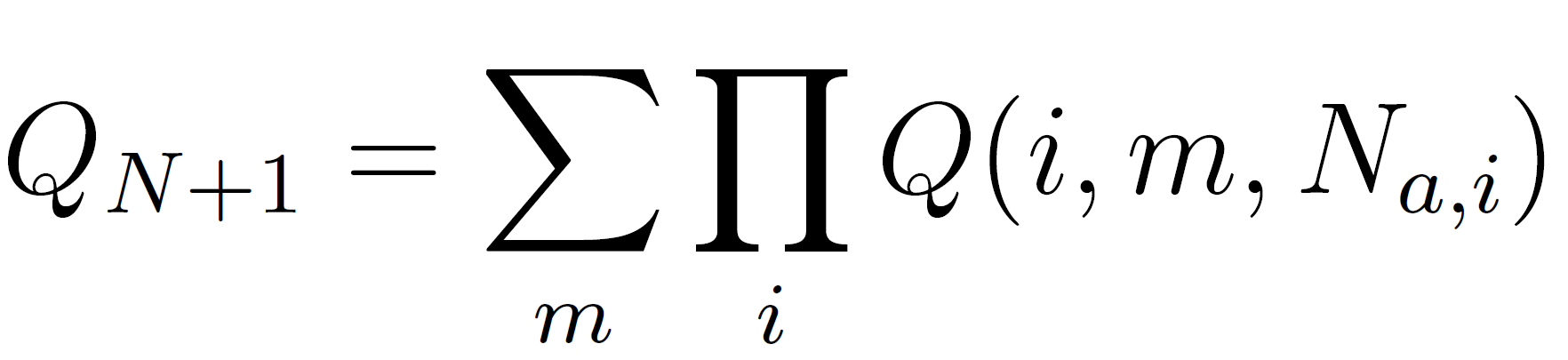
Again, each arm can be a homopolymer, copolymer or any other polymer. The partition function in all these cases can be calculated with the equations above.

Mean Number of Units in the Surface Layer

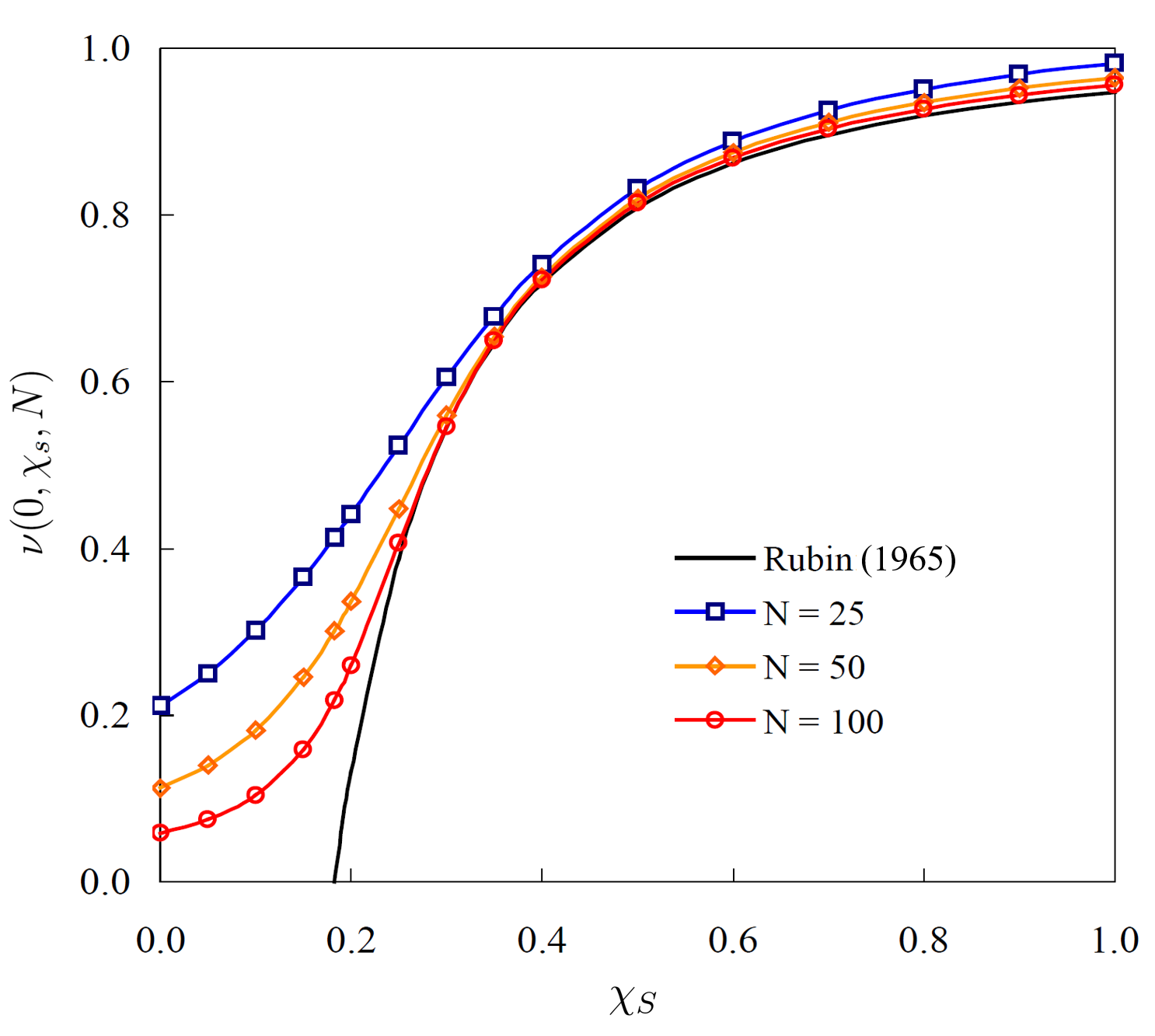
The Figure above shows the mean number of repeat units in the interface layer as a function of chain length N and adsorption parameter χ_s. The curves have been calculated with the lattice parameters of the simple cubic lattice: z = 6, λ₀ = 2/3, and λ₁ = 1/6. As can be seen from the curves, for long linear lattice chains and large adsorption parameters (χ_s > χ_s,c), the fraction of adsorbed repeat units, ν(0,χ_s,N), is nearly independent of the chain length N, whereas for weak adsorption, it depends strongly on the chain length.

References & Notes

1. P. J. Flory, J. Chem. Phys. 9, 660 (1941); 10, 51 (1942)
2. M. L. Huggins, J. Phys. Chem. 46, 151 (1942); J. Am. Chem. Soc. 64, 1712 (1942)
3. R. J. Rubin, J. Chem. Phys., 43, 2392 (1965)
4. E. A. DiMarzio and R. J. Rubin, J. Chem. Phys., 55, 4318 (1971)
5. E.A. Di Marzio, C.M. Guttman, A. Mah, Macromolecules 28, 2930 (1995)
6. R. J. Roe, J. Chem. Phys., 60, 4192 (1974)
7. J. M. H. M. Scheutjens & G. J. Fleer, J. Phys. Chem. 83, 1620 (1979) & 84, 178 (1980)

8. The matrix procedure, developed by Rubin and DiMarzio,^3-4 is only applicable to lattice polymers in the theta state.⁹ For all other cases, the matrix has to be modified to incorporate the effects of monomer-solvent interaction and excluded volume in each layer. This problem has been solved by Roe (1974)⁶ and Fleer and Scheutjens (1979).⁷